Refraktometr punktowy, którego zasadę działania pokazano na rys. l, jest urządzeniem bardzo prostym. Składa się z płaskiej nieprzezroczystej płytki z niewielkim otworem kołowym, białego ekranu (tła) i silnego źródła światła białego (światłowodowe źródło światła). Istotna dla jakości obrazów dyfrakcyjnych, a pośrednio dla dokładności pomiarów, jest średnica otworu (szerokość szczeliny), ponieważ od niej właśnie zależy kąt ugięcia. Im średnica otworu mniejsza, tym większy kąt ugięcia. Badania prowadzi się w czterech etapach, wyznaczając:
1) wartości współczynników załamania światła (n);
2) wartości dwójłomności (^);
3) dyspersji (D);
4) wartości ilorazu dwójłomności i dyspersji (^ /D).
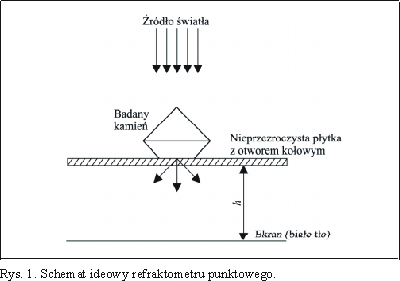
Sposób wykonania pomiarów jest następujący: badany kamień umieszcza się centrycznie nad otworem płytki, taflą w dół, i oświetla z góry silnym źródłem światła białego. Padające na kamień światło zostaje załamane i rozszczepione na granicy ośrodków powietrze - kamień i kamień - powietrze, a następnie, po wyjściu z kamienia, ugięte na krawędzi otworu płytki. W efekcie na białym ekranie pojawia się charakterystyczny obraz dyfrakcyjny w postaci barwnych pierścieni. Kształt otrzymanych obrazów i występowanie w nich pierścieni barwnych wynika z połączenia zjawisk dyfrakcji i interferencji światła. Kamienie jednołomne dają obraz dyfrakcyjny w postaci jednego wielobarwnego pierścienia, natomiast kamienie dwójłomne w postaci dwóch pierścieni.
Współczynnik załamania światła
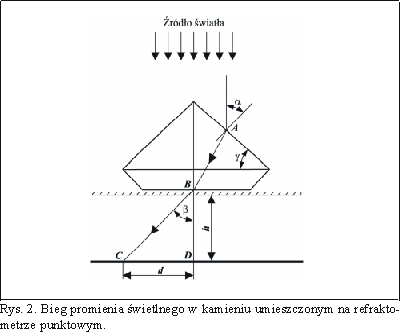
Pomiar współczynników załamania światła przy użyciu refraktometru punktowego stanowi najprostszą modyfikację metody refraktometrycznej stosowanej w praktyce gemmologicznej. Na rys. 2 pokazano bieg pojedynczego promienia światła monochromatycznego w badanym kamieniu. Na fasety pawilonu promień świetlny pada pod kątem alfa (prostopadle do tafli kamienia). W punkcie A, na granicy ośrodków (powietrze Ś kamień) promień ten zostaje załamany, następnie propaguje się w kamieniu wzdłuż odcinka AB i opuszcza kamień w punkcie B po powtórnym załamaniu na granicy ośrodków (kamień - powietrze). Do ekranu dociera przez mały kołowy otwór, na którym ulega ugięciu. Kąt załamania w punkcie B i kąt ugięcia na szczelinie jest równy kątowi beta. Wykorzystując prawa optyki falowej, można wyprowadzić zależność wiążącą kąty alfa i beta ze współczynnikiem załamania światła n:
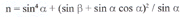
Z założenia równoległości biegu promieni świetlnych na drodze pomiędzy źródłem światła a kamieniem i ich prostopadłości do tafli kamienia wynika, że kąt a padania światła na fasety pawilonu jest równy kątowi g pawilonu. W związku z tym wzór (1) przybierze postać:
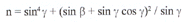
Zakładając, że kąt pawilonu gamma w stosunku do płaszczyzny rondysty, w poprawnie oszlifowanych kamieniach o bardzo dobrych lub dobrych proporcjach, jest stały (w praktyce ok. 40°) oraz że znana jest wartość h, możliwe jest wyznaczenie kąta beta z zależności:
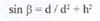
gdzie: d - promień barwnego pierścienia powstającego wskutek ugięcia światła na szczelinie; h - odległość płytki z otworem kołowym od ekranu (rys. 2).
Przyjmując, że kąt g dla badanych kamieni szlachetnych i ozdobnych o szlifie brylantowym jest stały, można uznać, że współczynnik załamania światła n zmienia się jedynie w funkcji kąta beta (pośrednio zależy od wartości d). Wynika stąd, że średnica barwnych pierścieni obserwowanych w metodzie Hodgkinsona jest funkcją współczynnika załamania światła danego kamienia, możliwe jest więc wyskalowanie odległości d na refraktometrze w jednostkach n . Skalowanie takie można przeprowadzić przy pomocy kamieni o znanym współczynniku załamania światła; w takim przypadku miarą n będzie zawsze odległość mierzona od osi barwnego pierścienia (punkt D na rys. 2) do pierścienia o barwie żółtej.
Dwójłomność ^
Kamienie dwójłomne badane za pomocą refraktometru punktowego dają dwa obrazy dyfrakcyjne, które w zależności od wartości dwójłomności mogą zajmować względem siebie trzy różne położenia:
1) obrazy dyfrakcyjne są wyraźnie rozdzielone (duża dwójłomność, np. oliwin ^ = 0,036); 2) obrazy dyfrakcyjne pokrywają się w pewnym zakresie (średnia wartość dwójłomności, np. turmalin ^ = 0,020);
3) obrazy dyfrakcyjne pokrywają się prawie całkowicie (mała dwójłomność, np. apatyt ^ = 0,003);
W pierwszym i drugim przypadku, używając "cechowanej" skali refraktometru punktowego, można określić wartości współczynnika załamania światła dla żółtej barwy dwóch pierścieni pojawiających się w obrazie dyfrakcyjnym, przy czym różnica tych wartości stanowić będzie wartość liczbową dwójłomności. Dla przypadku trzeciego, gdy obrazy dyfrakcyjne pokrywają się ze sobą, precyzyjne ustalenie położenia barwy żółtej w widmie jest bardzo trudne. Dobre wyniki można uzyskać, wykonując pomiar pomiędzy położeniami pierścieni o barwie czerwonej. Odpowiada to w pewnym sensie zastosowaniu czerwonego filtra w pomiarach refraktometrycznych i choć bezwzględne wartości współczynników za- łamania światła dla światła czerwonego i żółtego są różne, jednak uzyskana w ten sposób wartość dwójłomności wyznaczanej metodą Hodgkinsona zależy od położenia kamienia względem źródła światła, kątów, jakie tworzą osie optyczne z taflą kamienia, i kąta obserwacji, dlatego pomiar należy powtarzać kilkakrotnie; za wartość diagnostyczną przyjmuje się maksymalną wartość dwójłomności.
Dyspersja
W refraktometrze punktowym odpowiednio wyskalowanym w jednostkach n wartość dyspersji określa się jako różnicę odległości pomiędzy pierścieniem czerwonym a niebieskim danego obrazu dyfrakcyjnego (odpowiada to liniom Fraunhofera B-G). Należy pamiętać, że dla kamieni dwójłomnych, o dwóch obrazach, wartość dyspersji powinna być liczona pomiędzy pierścieniem czerwonym i niebieskim tego samego obrazu.
Stosunek dwójłomności do dyspersji (^ /D)
Określenie stosunku ^ /D sprowadza się do znalezienia jego maksymalnej wartości. Ponieważ wartość dyspersji jest niezależna od ustawienia kamienia względem źródła światła i położenia płaszczyzny tafli w stosunku do osi optycznych, wyznaczenie maksimum wartości ^ /D zależy jedynie od poprawnego wyznaczenia maksymalnej wartości dwójłomności. Wartość ta jest proporcjonalna do odległości pomiędzy pierścieniami żółtymi lub czerwonymi obserwowanych obrazów, natomiast D jest proporcjonalna do odległości między zewnętrznym pierścieniem czerwonym i wewnętrznym pierścieniem niebieskim danego obrazu. Z praktyki gemmologicznej wiadomo, że w tym zakresie widma wartości ^/D zmieniają się nieliniowo od wartości 0 dla kamieni izotropowych do wartości 2,6 dla kamieni anizotropowych. W tabeli zestawiono przykłady wartości n, ^, D i stosunku ^ /D dla wybranych kamieni szlachetnych i ozdobnych.
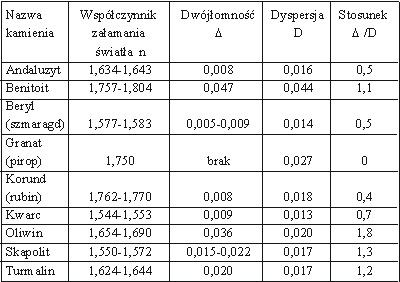
Tab. Przykłady wartości n, ^, D i stosunku ^ / D dla wybranych kamieni szlachetnych
Wnioski
Metoda Hodgkinsona ze względu na swoją prostotę jest godna rozpowszechnienia. Nie wymaga stosowania kosztownych przyrządów pomiarowych, a mimo to daje możliwość bezpośredniego porównania wielkości n, ^ i D, co zaawansowanym gemmologom pozwala na szybką i bezbłędną identyfikację kamieni. Proponowana metoda ma jednak pewne ograniczenia. Ponieważ poprawność wyników badań zależy od jakości uzyskiwanych obrazów dyfrakcyjnych, wpływ na otrzymywane dane mają następujące czynniki:
(1) rodzaj i forma szlifu - stąd ograniczenie metody do okrągłych szlifów brylantowych i ich modyfikacji;
(2) proporcje szlifu Ś z założenia wymagane bardzo dobre lub dobre;
(3) Źródło światła - wymagane jest silne źródło światła białego ustawione tak, by czoło fali było prostopadłe do tafli badanego kamienia;
(4) kąt osi optycznych w stosunku do tafli kamienia - kamienie jednoosiowe o osi optycznej prostopadłej do tafli kamienia dają na refraktometrze identyczny odczyt jak kamienie izotropowe; w przypadku stosowania metody Hodgkinsona można otrzymać tylko jeden obraz dyfrakcyjny;
(5) wielkość kamienia - wraz ze wzrostem wymiarów kamienia polepsza się jakość otrzymywanych obrazów;
(6) barwa kamienia - kamienie o intensywnej barwie własnej absorbują promieniowanie o określonych długościach fal (selektywna absorpcja światła), "wycinając" z obserwowanego widma całe zakresy barwne, np. barwę żółtą (kamienie intensywnie niebieskie, indygo i fioletowe), czerwoną (kamienie niebieskozielone) lub niebieską (kamienie pomarańczowe).
Literatura:
W. Hanneman: Educating the Eyeball - the Hodgkinson Method. "Lapidary Journa". 1980 nr 7.
W. Hanneman: Understanding the Hodgkinson Method. "Journal of Gem- mology" 1991 nr 3.
A. Hodgkinson: Visual Optics. "Journal of Gemmology" 1979 nr 5.
T. Sobczak, N. Sobczak: Niekonwencjonalne metody badania kamieni szlachetnych. "Acta Univesitatis Wratislaviensis" 1996 nr 1784.
|


